POR
O que um grande filósofo grego tem a ver com um grupo de cinco poliedros regulares?
Tudo, especialmente se o personagem em questão se chama Platão e se considerarmos a natureza extremamente conceitual da geometria.
Mas de que poliedros estamos falando exatamente?
É preciso ser preciso: os cinco sólidos platônicos, de fato, têm algumas características que ninguém mais possui.
A primeira é que eles são formados apenas por polígonos regulares, especificamente por triângulos equiláteros, quadrados ou pentágonos.
Em particular, o tetraedro, octaedro e icosaedro são formados por quatro, oito e vinte triângulos, respectivamente, o hexaedro (ou cubo) por seis quadrados, e o dodecaedro por doze pentágonos.
Mas uma segunda característica também é necessária, que é que os anguloides, ou seja, os ângulos sólidos fechados entre três ou mais lados, são todos iguais entre si.
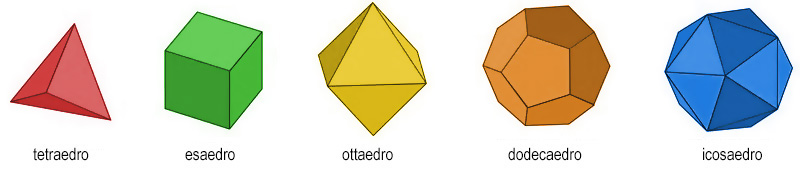
Os sólidos platônicos, além disso, são os únicos poliedros convexos que podem ser inscritos em uma esfera, ou seja, eles têm todos os vértices situados na superfície da própria esfera.
O encanto destes poliedros e a sua singularidade já eram apreciados nos tempos antigos.
Parece que Pitágoras já havia descoberto as propriedades das "figuras cósmicas", enquanto Platão as associava aos elementos fundamentais.
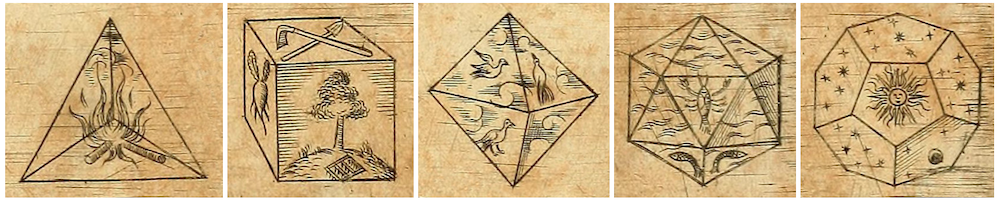
No "Timeu" (360 a.C.) ele conecta o tetraedro ao fogo, o cubo à terra, o octaedro ao ar e o icosaedro à água.
O dodecaedro, por outro lado, é um símbolo do universo.
Essa atribuição especial deriva da presença do pentágono, uma figura que – contendo a proporção áurea – continha mais do que qualquer outra a ideia de harmonia e perfeição matemática.
Os cinco poliedros retornam com uma abordagem mais matemática no décimo terceiro livro dos "Elementos" de Euclides (300 a.C.).
O estudioso conseguiu demonstrar que não poderia haver mais do que cinco poliedros regulares e identificou as fórmulas para calcular a borda, o volume e a superfície em relação ao diâmetro da esfera circunscrita.

No entanto, antes da Grécia antiga, os sólidos platônicos já haviam aparecido no Neolítico na forma de pedras arredondadas (chamadas petroesferas) encontradas na Escócia e datadas de 2.000 a.C.
O número de "botões" na superfície refere-se, na maioria dos espécimes, ao número de faces dos sólidos platônicos.

Si tratta di oggetti piuttosto misteriosi, così come i dodecaedri romani, strani solidi metallici dotati di piccole sfere lungo i vertici e grossi fori al centro di ogni faccia.

Dopo l’età classica i solidi platonici tornano in voga – ovviamente – nel Rinascimento.
Stavolta però, oltre i matematici, interessano anche gli artisti.
Tra i primi va ricordato Paolo Uccello, pittore ed esperto di prospettiva che sul pavimento della basilica di San Marco a Venezia ha realizzato intorno al 1430 una splendida tarsia marmorea con il disegno di un inedito dodecaedro stellato (cioè dotato di una piramide su ogni faccia).

Piero della Francesca dedica ai cinque poliedri un intero trattato dal titolo “De quinque corporibus regularibuNel testo, scritto intorno al 1480, il pittore sostiene che il mondo è costituito da volumi di forme complesse e irregolari ma che sono tutti riconducibili ai solidi platonici, forme basilari eterne e perfette.
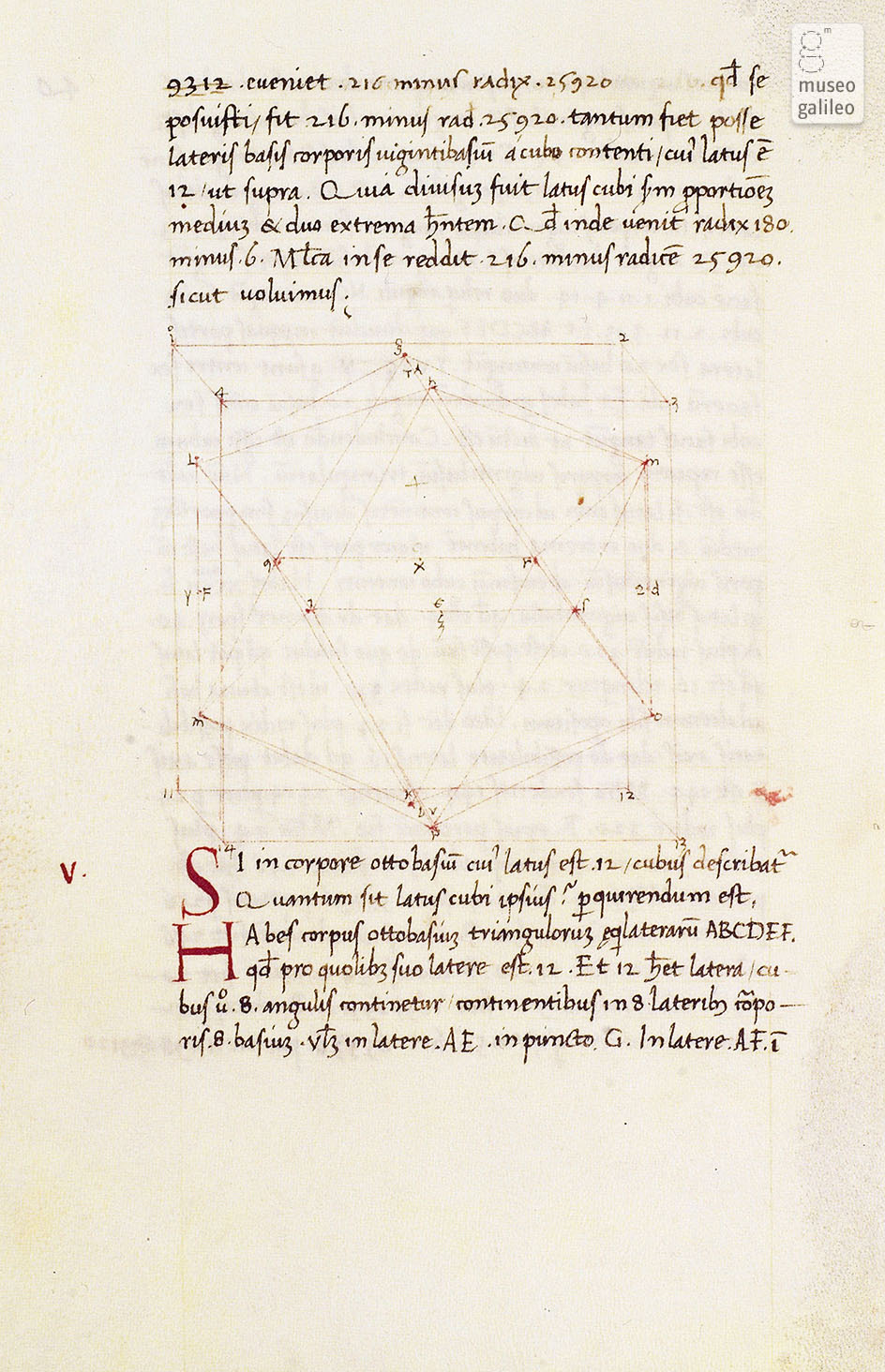
Pochi anni dopo Leonardo da Vinci disegna i solidi platonici, assieme a tanti altri poliedri, a corredo del “De divina proportione” (1509) del matematico Luca Pacioli.
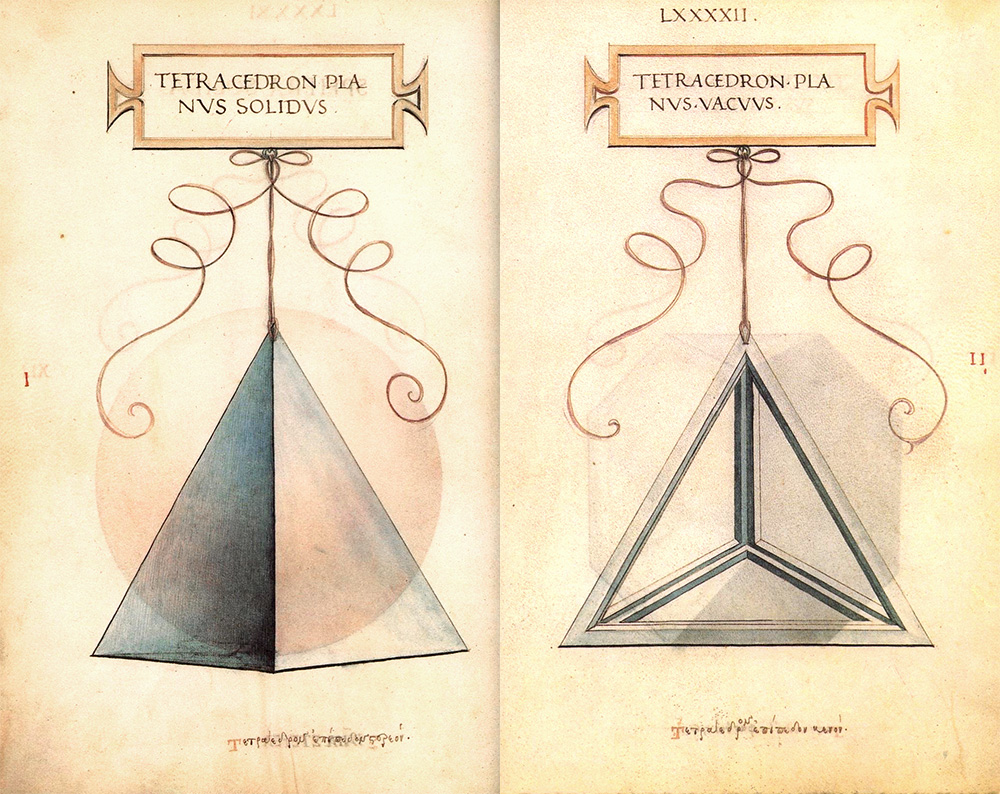
Nei suoi splendidi acquerelli ogni poliedro è appeso con una cordicella ad un cartiglio recante il nome latino del solido stesso (alla base del foglio, invece, è riportato il nome in greco).
Di ognuno ha realizzato una versione piena (solidus) e una vuota (vacuus). Ecco il tetracedron.
Segue l’exacedron.
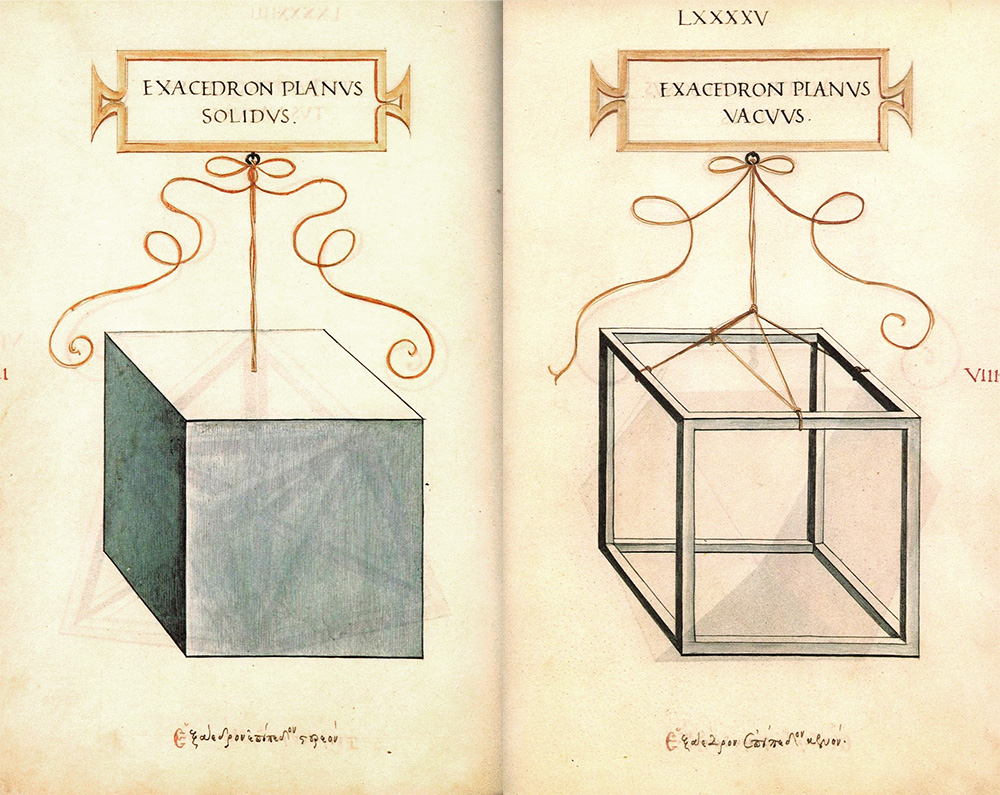
Poi c’è l’octocedron.
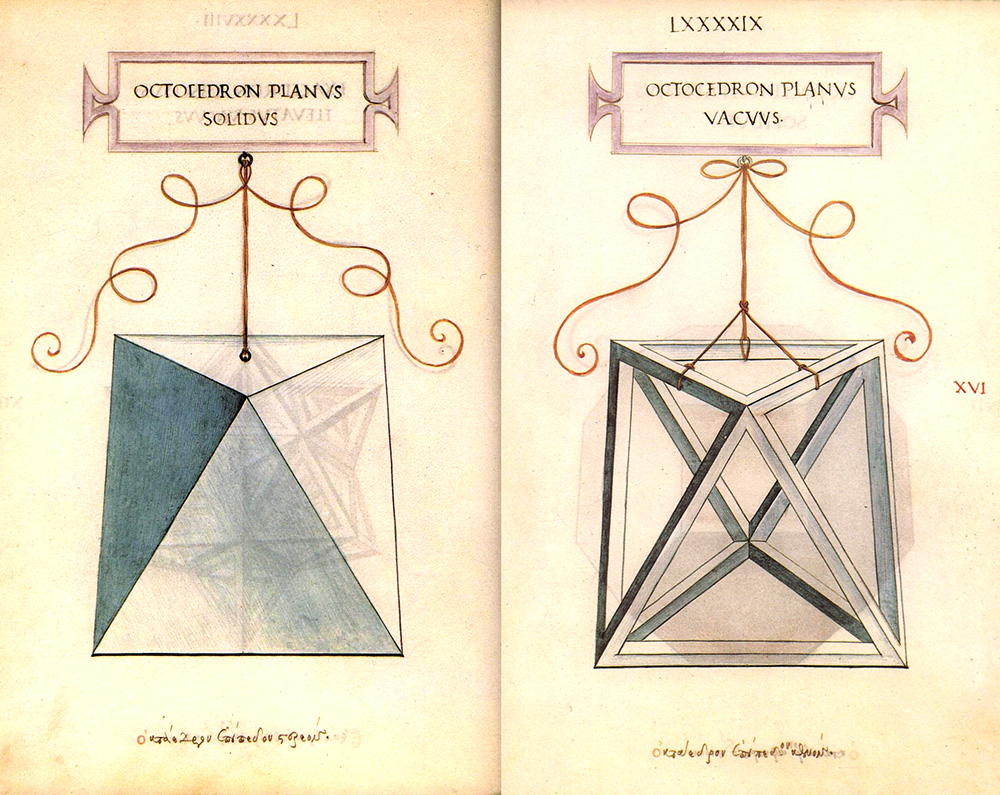
E ancora il duodecedron.
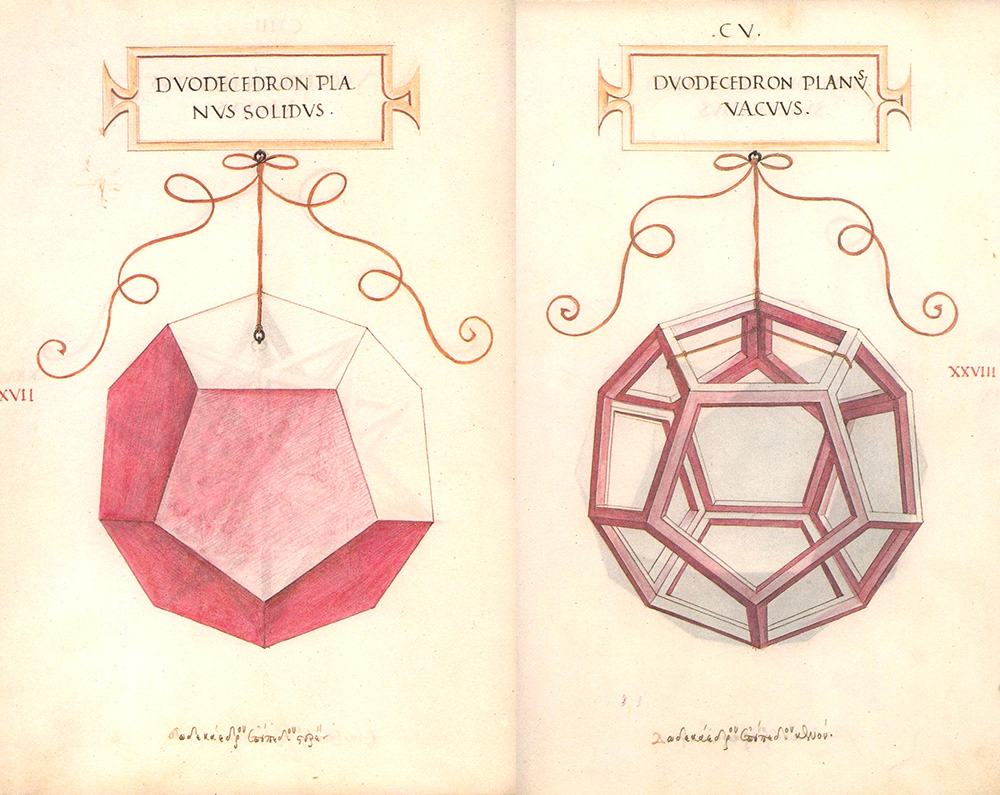
E infine l’ycocedron.
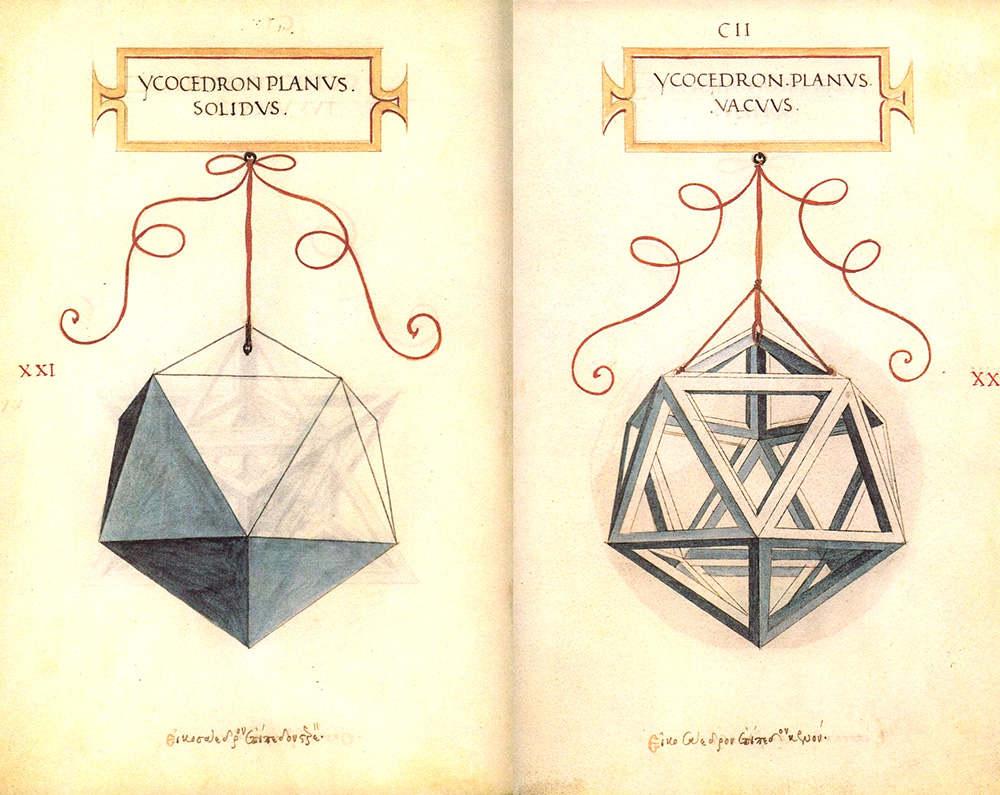
Pochi anni dopo anche il tedesco Albrecht Dürer si occupa di poliedri.
È celebre quello presente nell’incisione Melancolia I del 1514. Non è un solido platonico ma sembra averne tutto il fascino.

Posteriormente, com seu "Underweysung der Messung mit dem Zirckel und Richtscheyt" (1525) (Instruções para medir com régua e bússola), Dürer esboça o desenvolvimento de alguns poliedros, ou seja, a figura plana obtida pela separação de algumas arestas entre as faces.
Aqui está o desenvolvimento do dodecaedro e suas vistas do lado e de cima.
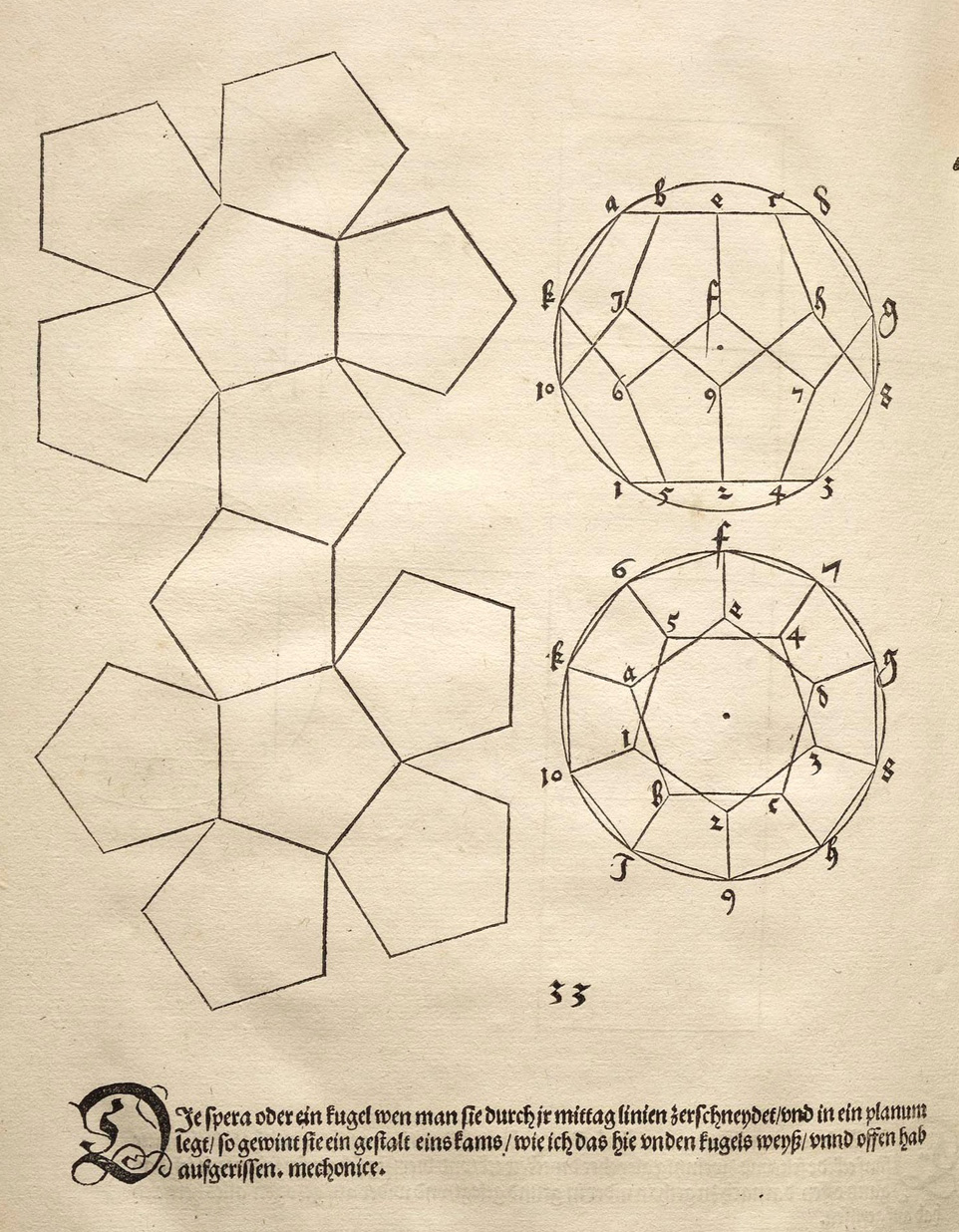
Algo semelhante também foi produzido por Augustin Hirschvogel, um artista e matemático alemão, autor do tratado "Geometria" (1543) que ele mesmo ilustrou.
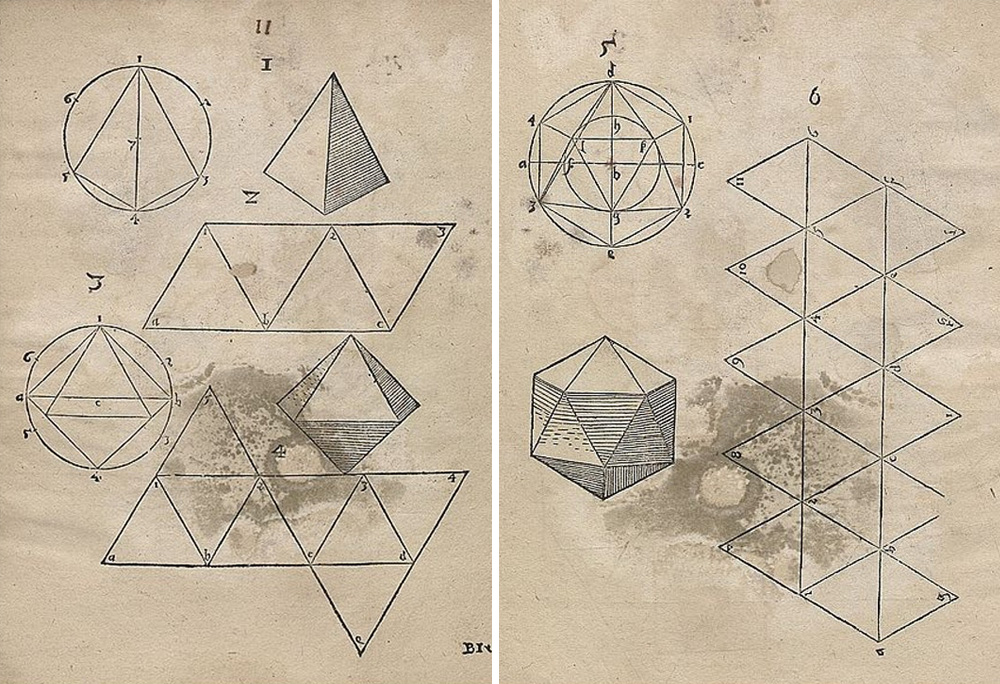
Decididamente mais artísticas são as placas de Lorenz Stoer contidas em sua Geometria et Perspectiva (1567).
Neste caso, os sólidos platônicos estão situados dentro de paisagens geométricas que parecem antecipar as visões matemáticas de Escher.

Após meados do século, foi a vez do gravador alemão Wenzel Jamnitzer, que em sua "Perspectiva corporum regularium" (1568) analisou todas as possíveis variantes dos cinco sólidos platônicos, incluindo as versões estreladas ou truncadas (ou seja, com os vértices cortados).
O total é de 120 poliedros: uma coleção imaginativa de formas impensáveis que está exatamente a meio caminho entre a ciência e a arte e que quer demonstrar a suposição de Platão de que todo sólido descende dos cinco originais.
Estas são duas tabelas com algumas variações sobre o icosaedro.
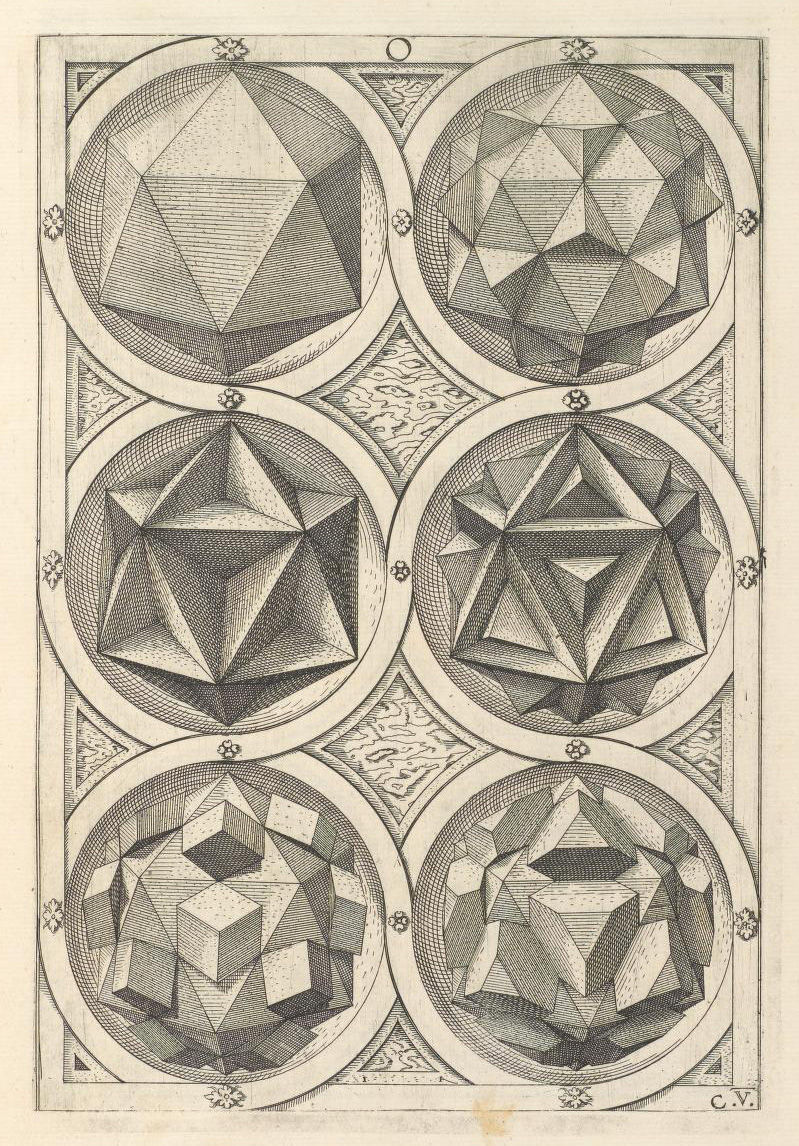

Embora estes sejam alguns exemplos de variações dodecaedros.
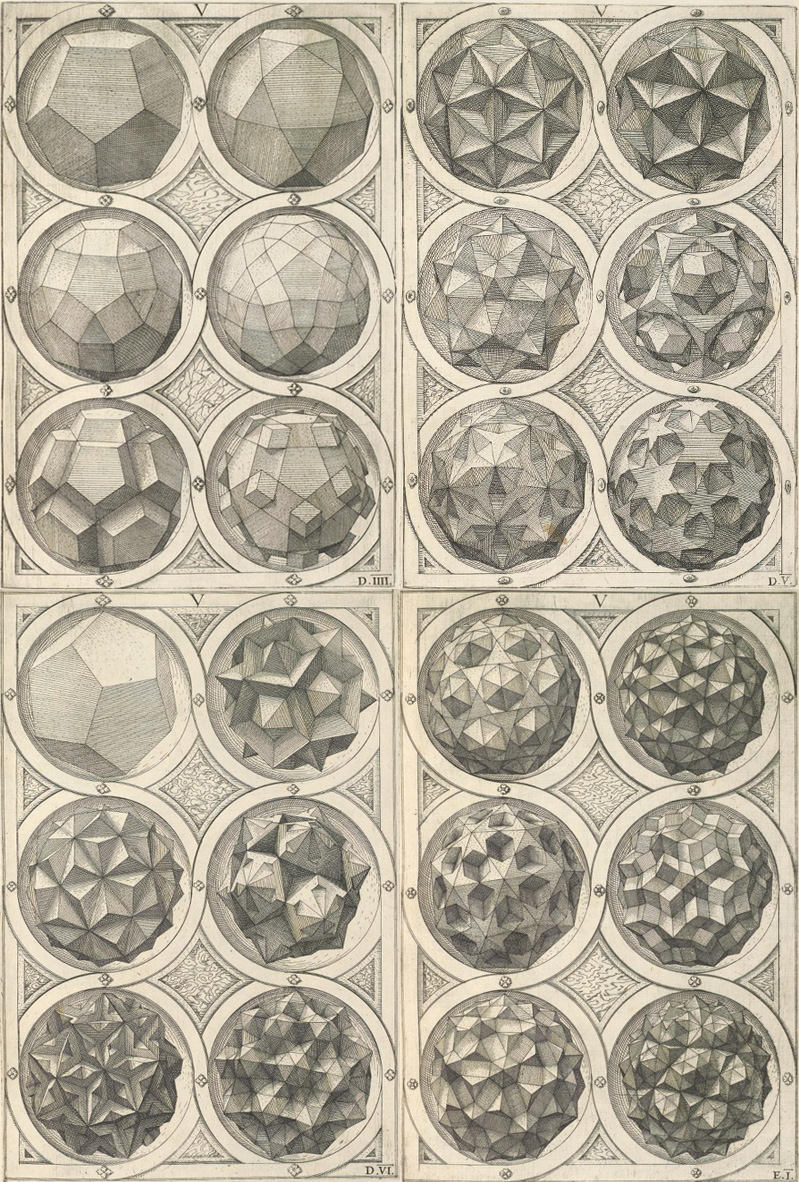
Observar esses desenhos é experimentar visualmente a vertigem do cálculo combinatório, com a diferença de que as possibilidades de transformação dos sólidos platônicos são potencialmente infinitas.
Do mesmo período, mas de um artista desconhecido, são alguns desenhos em aquarela em que poliedros mais ou menos complexos são acompanhados por pássaros ou outros pequenos animais.
O efeito, delicado e alienante ao mesmo tempo, é incrivelmente surreal.

Pochi anni dopo, le teorie di Platone verranno riprese da Keplero che nel suo “Mysterium Cosmographicum” (1597) immagina il sistema solare come un insieme concentrico di solidi platonici, le cui proporzioni determinano le distanze e le posizioni dei pianeti.
La rappresentazione grafica di questo concetto è stata realizzata da Christophorus Leibfried.
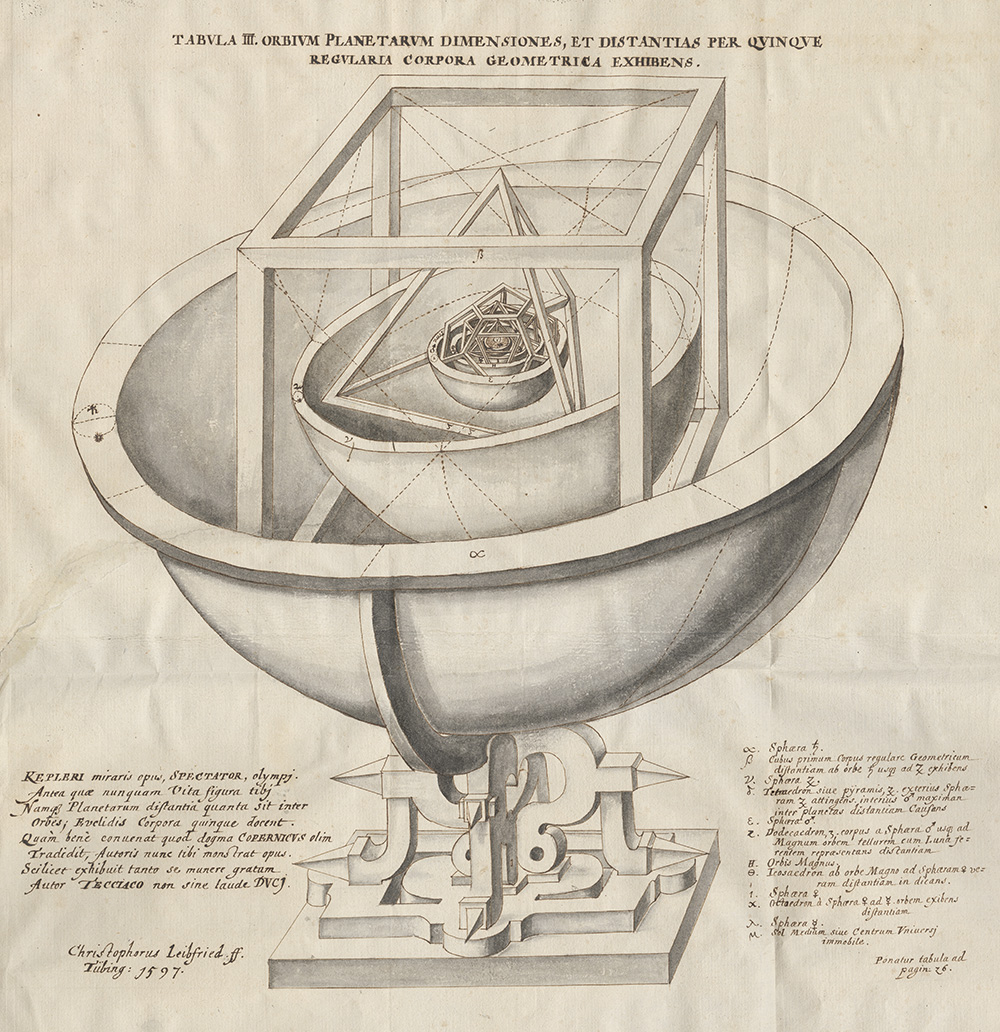
Con “Harmonices Mundi” del 1619 Keplero torna ad occuparsi dei solidi platonici alla ricerca del concetto di armonia e bellezza geometrica.
È in questo testo che teorizza i poliedri non convessi (inclusi quelli stellati) che oggi portano il suo nome.

Nel 1900 è la volta del matematico tedesco Max Brücker, autore di “Vielecke und Vielflache: Theorie und Geschichte” (Poligoni e poliedri: teoria e storia).
Il suo testo, una summa di tutto ciò che si sapeva fino a quel momento sulla materia, è accompagnato da centinaia di incisioni e dalle foto di 146 spettacolari modelli in carta dei vari solidi.

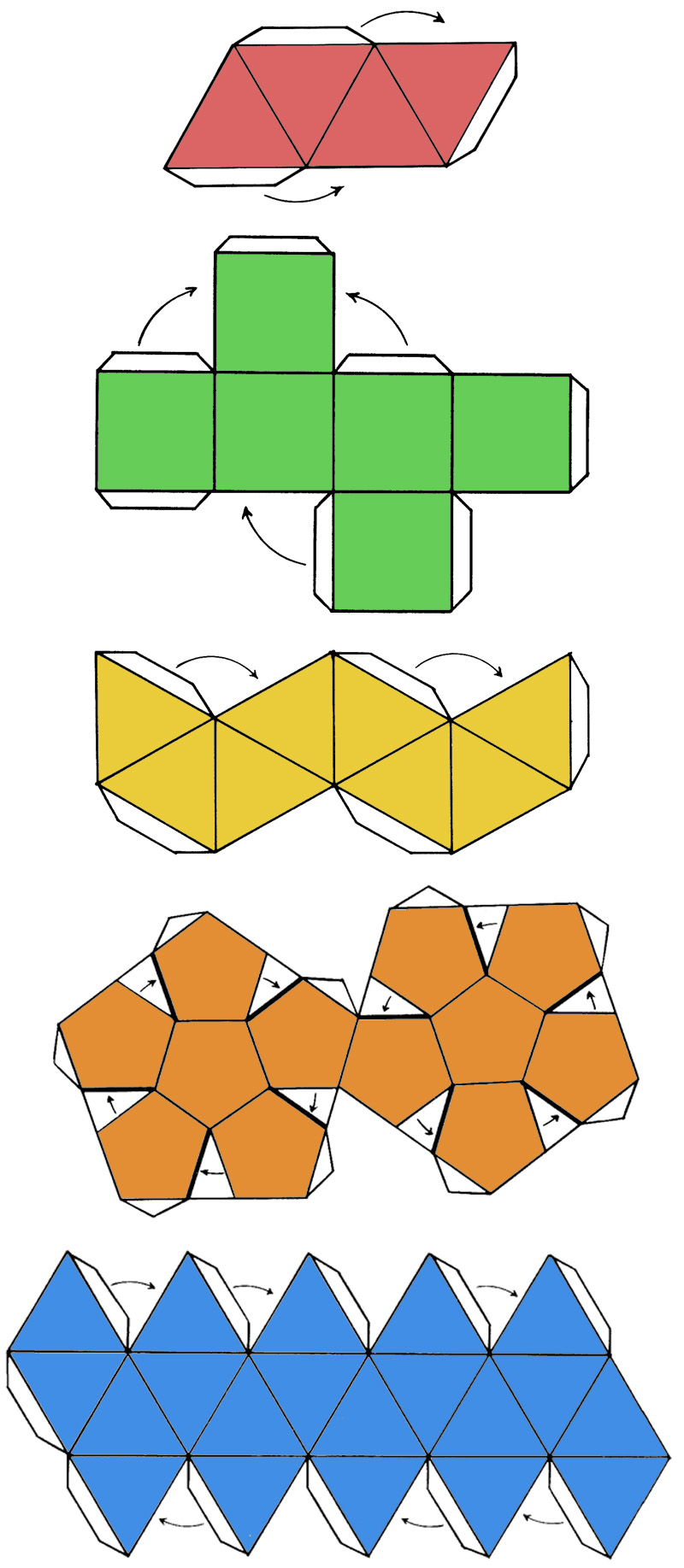
Quella del modellino tridimensionale è un’attività che, in piccolo, si può fare anche a scuola.
Basta disegnare su carta lo sviluppo dei solidi con le apposite linguette e incollare i vari lati. L’importante è essere estremamente precisi nella geometria delle varie facce.

I solidi platonici e le loro versioni stellate saranno una delle passioni di Maurits Cornelis Escher.
E proprio “Stelle” si intitola una xilografia del 1948 in cui l’artista olandese mette assieme il camaleonte, simbolo di trasformazione, il concetto platonico di eterna perfezione dei poliedri e l’evocazione del cosmo.
Il solido centrale, vuoto come quelli di Leonardo, è un originale incastro di tre ottaedri.

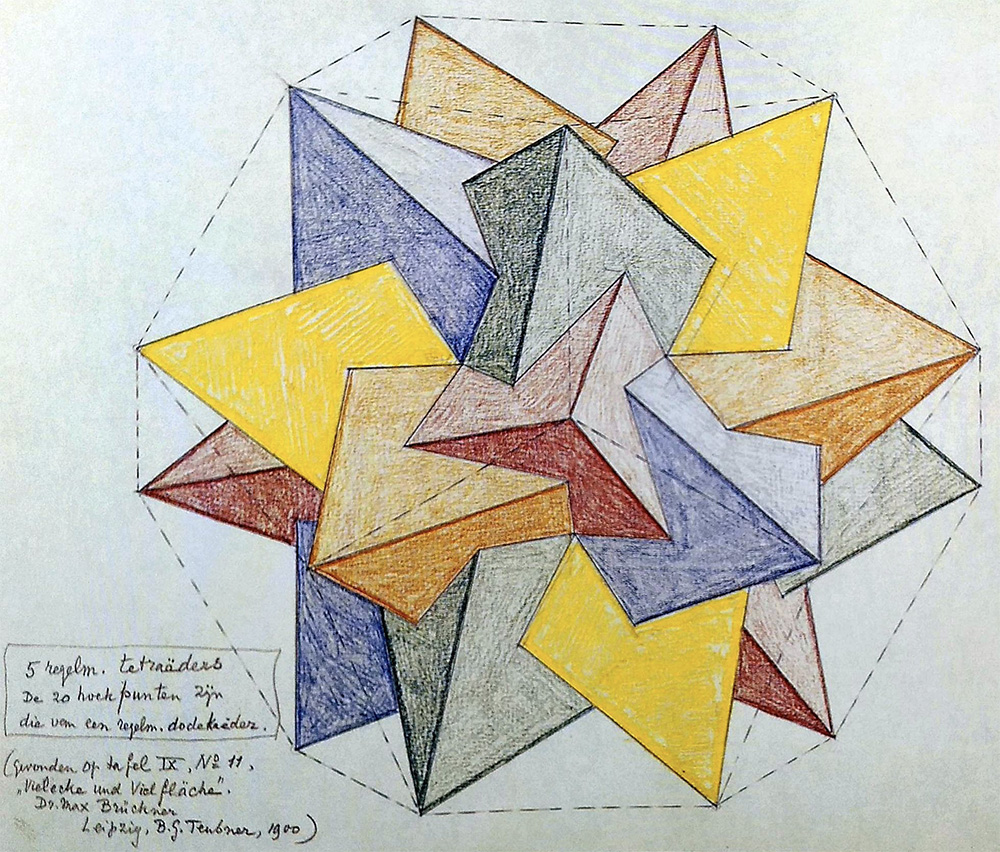
Quello di “Stelle” non è l’unico poliedro nato da un incastro. In questo schizzo Escher è riuscito a mettere assieme ben cinque tetraedri!
Solo grazie al colore riusciamo a individuare i singoli solidi che lo compongono.
Con “Cristallo”, del 1947, Escher incastra un cubo e un ottaedro per creare un oggetto dalla geometria purissima da contrapporre alla massa informe della ghiaia.
Di questi solidi quasi astratti l’artista diceva: “Essi simbolizzano il desiderio di armonia e di ordine dell’uomo, ma nello stesso tempo la loro perfezione desta in noi il senso della nostra impotenza. I poliedri regolari non sono invenzioni della mente umana, perché esistevano molto prima che l’uomo comparisse sulla scena“.

La stessa esaltazione della perfezione dei poliedri è il tema di “Contrasto (ordine e caos)” del 1950. Il solido, un dodecaedro stellato quasi trasparente, è parzialmente inglobato in una sfera di vetro.
Attorno a questo simbolo di bellezza matematica solo oggetti rotti, a rappresentare il caos che si contrappone all’ordine.

In tempi più recenti si trovano i dipinti di Lucio Saffaro, pittore, scrittore e matematico che tra gli anni Ottanta e Novanta ha fatto dei solidi platonici e delle loro varianti i soggetti unici di tele dal sapore metafisico.

Esses sólidos, tão claros, tão absolutos, confirmam o pensamento de Bertrand Russell sobre a relação entre matemática e arte:
"A matemática, vista do ângulo reto, possui não apenas a verdade, mas também a beleza suprema, uma beleza fria e austera, como a da escultura, sublimemente pura e capaz de uma perfeição austera, como só a grande arte pode mostrar".

Comentários
Postar um comentário